关于λ演算的初步解析

序言

学算法的时候，就了解过图灵完备（Turing Complete），Steam上也有一款游戏叫做图灵完备，要是我大学早一点发现这个游戏我的计组和计体中的汇编就不会学得很痛苦了，那是一款从0开始教你从最初的与非门搭建到一台图灵完备可编程计算机的游戏，目前没通关，卡在了处理器架构2的有符号小于实现的关卡处（还是太菜了，加上自己比较逞强，又不想看攻略，就长时间卡关，甚是惭愧），因为不管是日常工作编程的 Java 还是机器学习代码中 都有用到lambda演算的技巧，于是，我去查了这个λ演算到底是怎么个原理，为什么说λ演算是和图灵机等价的，然后笔者写下了这篇文章。

背景

λ演算（Lambda Calculus）是计算机科学和数学逻辑中的一个基础理论体系，由数学家阿隆佐·丘奇（Alonzo Church）在20世纪30年代提出。作为一种形式化的数学系统，λ演算为函数定义、函数应用和递归提供了简洁而强大的表达方式，成为了现代编程语言理论的基石。笔者将从最最基础概念出发，逐步解析λ演算的核心思想、与图灵机的等价性以及在现代编程语言中的应用。

1. λ演算的基本概念

1.1 语法结构

λ演算的语法真滴非常简洁，就仅由三种基本元素构成：

• 变量：用于表示参数或自由变量
• 抽象：定义一个函数，形式为 $\lambda x.M$，其中 $x$ 是参数，$M$ 是函数体
• 应用：将函数应用于参数，形式为 $(M N)$，其中 $M$ 是函数，$N$ 是参数

然后，形式化地，λ项（lambda term）可以用BNF（巴科斯范式）表示为：

$$ \begin{align} \text{term} &::= \text{variable} \\ &| \lambda\text{variable}.\text{term} \\ &| (\text{term } \text{term}) \end{align} $$

1.2 求值规则

λ演算的核心是β-归约（beta-reduction），这是表示函数应用时的计算规则：

$$(\lambda x.M)N \rightarrow M[x := N]$$

其中 $M[x := N]$ 表示将 $M$ 中所有自由出现的 $x$ 替换为 $N$。

α-转换（alpha-conversion）则允许咱重命名绑定变量：

$$\lambda x.M \equiv \lambda y.M[x := y]$$

η-转换（eta-conversion）表达了外延性原则：

$$\lambda x.(M x) \equiv M \quad \text{若 } x \text{ 不在 } M \text{ 中自由出现}$$

2. λ演算中的数据表示

2.1 丘奇数

在λ演算中，自然数可以用丘奇数（Church numerals）表示，这是一种将自然数编码为高阶函数的方法：

$$ \begin{align} 0 &= \lambda f.\lambda x.x \\ 1 &= \lambda f.\lambda x.f(x) \\ 2 &= \lambda f.\lambda x.f(f(x)) \\ n &= \lambda f.\lambda x.f^n(x) \end{align} $$

丘奇数 $n$ 本质上是一个接受函数 $f$ 和参数 $x$，然后将 $f$ 应用于 $x$ 共 $n$ 次的高阶函数。

2.2 布尔值和条件表达式

布尔值可以表示为：

$$ \begin{align} \text{TRUE} &= \lambda x.\lambda y.x \\ \text{FALSE} &= \lambda x.\lambda y.y \end{align} $$

条件表达式可以定义为：

$$\text{IF} = \lambda p.\lambda a.\lambda b.p \, a \, b$$

3. λ演算的计算能力

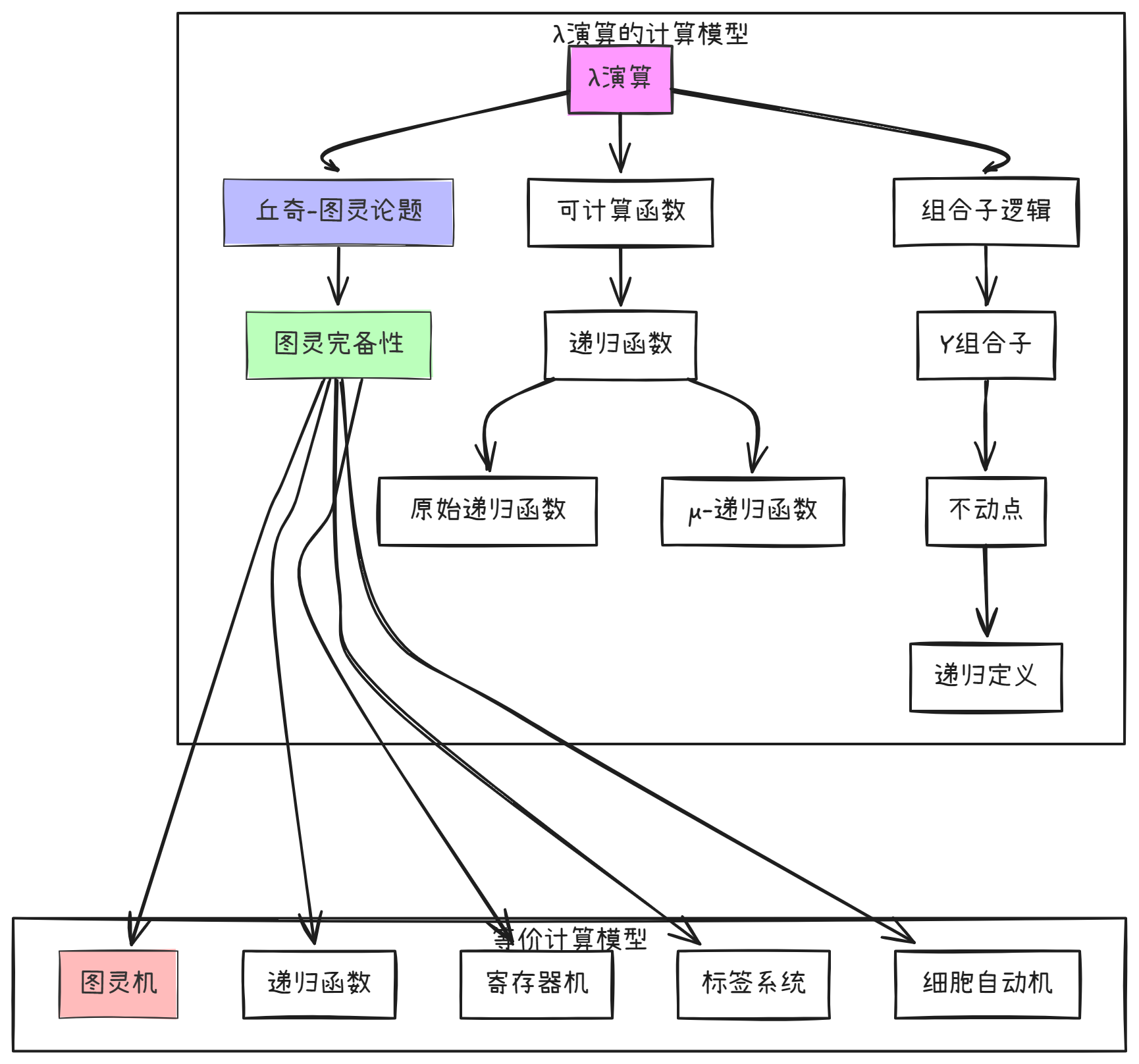
3.1 Y组合子与递归

λ演算中没有内置的递归机制，但可以通过Y组合子（fixed-point combinator）实现递归：

$$Y = \lambda f.(\lambda x.f(x \, x))(\lambda x.f(x \, x))$$

Y组合子满足等式 $Y \, f = f \, (Y \, f)$，这使得 $Y \, f$ 成为函数 $f$ 的不动点，从而实现递归。

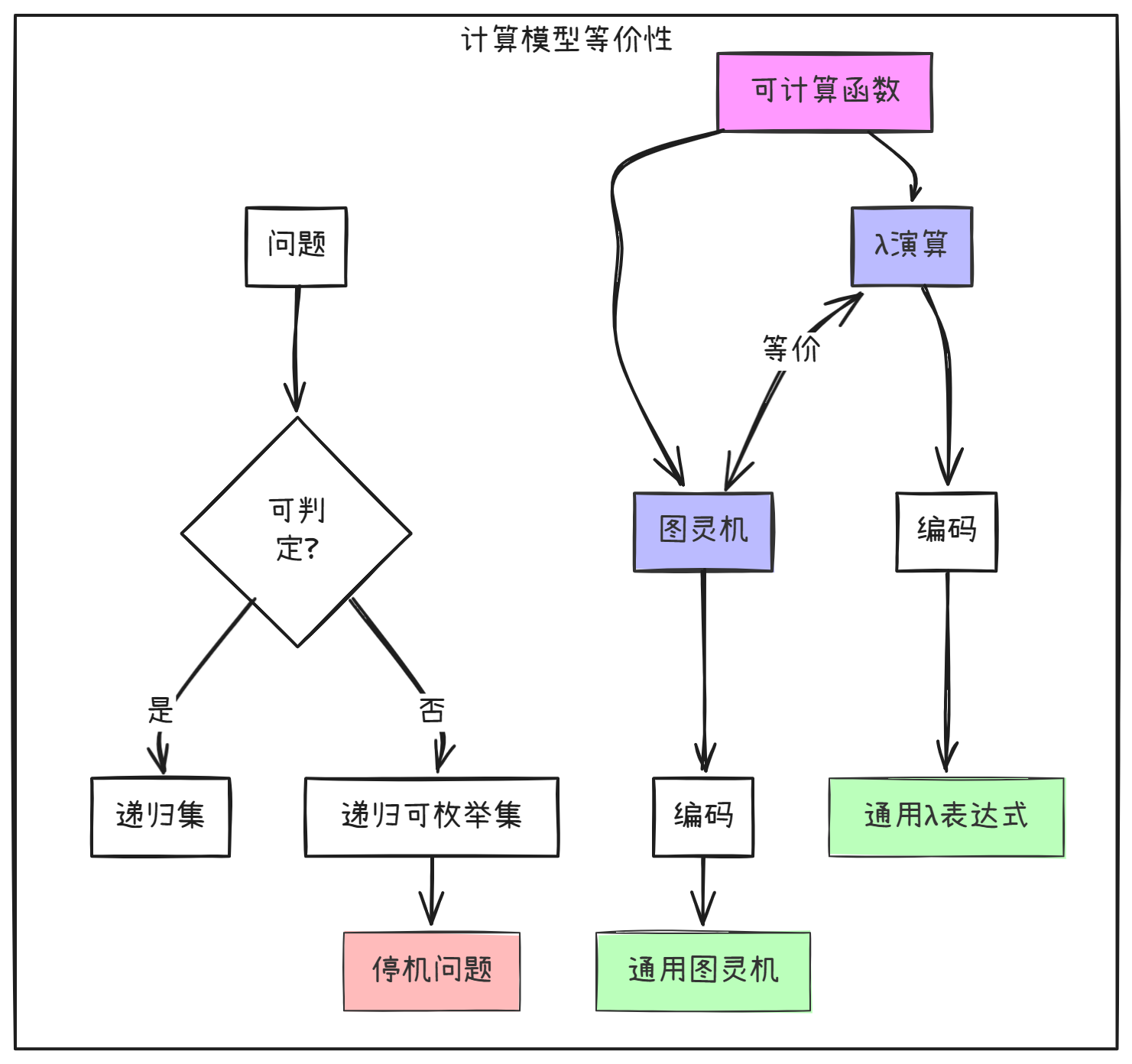
3.2 λ演算与图灵机的等价性

丘奇-图灵论题（Church-Turing thesis）指出，任何可计算函数都可以通过λ演算或图灵机计算。这两种计算模型在计算能力上是等价的，但是它们的形式和操作方式不能说不太像，只能说完全不同。

4. λ演算的类型系统

4.1 简单类型λ演算

简单类型λ演算（Simply Typed Lambda Calculus, STLC）引入了类型约束，基本类型和函数类型的语法如下：

$$ \begin{align} \tau ::= \alpha \mid \tau_1 \rightarrow \tau_2 \end{align} $$

其中 $\alpha$ 是基本类型，$\tau_1 \rightarrow \tau_2$ 是函数类型。

类型判断规则可以表示为：

$$ \frac{\Gamma, x:\sigma \vdash M : \tau}{\Gamma \vdash \lambda x:\sigma.M : \sigma \rightarrow \tau} \text{(Abs)} $$

$$ \frac{\Gamma \vdash M : \sigma \rightarrow \tau \quad \Gamma \vdash N : \sigma}{\Gamma \vdash M \, N : \tau} \text{(App)} $$

4.2 多态λ演算与系统F

系统F（System F）引入了多态类型，允许类型变量的量化：

$$ \begin{align} \tau ::= \alpha \mid \tau_1 \rightarrow \tau_2 \mid \forall \alpha. \tau \end{align} $$

其中 $\forall \alpha. \tau$ 表示对所有类型 $\alpha$，表达式都具有类型 $\tau$。

5. λ演算在编程语言中的应用

5.1 函数式编程语言

函数式编程语言如Haskell、ML、Lisp等主FP范式的编程语言直接受到λ演算的影响，于是，我拿出小学二年级就学过的Python简单模拟了个λ演算：

# λ演算解释器
class Expr:
    pass

class Var(Expr):
    def __init__(self, name):
        self.name = name
    
    def __str__(self):
        return self.name
    
    def eval(self, env):
        return env.get(self.name, self)
    
    def subst(self, var, expr):
        return expr if self.name == var else self

class Abs(Expr):
    def __init__(self, var, body):
        self.var = var
        self.body = body
    
    def __str__(self):
        return f"(λ{self.var}.{self.body})"
    
    def eval(self, env):
        return self
    
    def subst(self, var, expr):
        if var == self.var:
            return self
        else:
            return Abs(self.var, self.body.subst(var, expr))

class App(Expr):
    def __init__(self, func, arg):
        self.func = func
        self.arg = arg
    
    def __str__(self):
        return f"({self.func} {self.arg})"
    
    def eval(self, env):
        func = self.func.eval(env)
        arg = self.arg.eval(env)
        
        if isinstance(func, Abs):
            return func.body.subst(func.var, arg).eval(env)
        else:
            return App(func, arg)
    
    def subst(self, var, expr):
        return App(self.func.subst(var, expr), self.arg.subst(var, expr))

# 丘奇数
def church_numeral(n):
    var_f = Var("f")
    var_x = Var("x")
    body = var_x
    for _ in range(n):
        body = App(var_f, body)
    return Abs("f", Abs("x", body))

# 测试
zero = church_numeral(0)
one = church_numeral(1)
two = church_numeral(2)
print(f"Church 0: {zero}")
print(f"Church 1: {one}")
print(f"Church 2: {two}")

# Y组合子
Y = Abs("f", 
        App(Abs("x", App(Var("f"), App(Var("x"), Var("x")))),
            Abs("x", App(Var("f"), App(Var("x"), Var("x"))))))
print(f"Y组合子: {Y}")

5.2 类型推导

现代编程语言中的类型推导算法（如Hindley-Milner算法）就源自λ演算的类型系统研究：

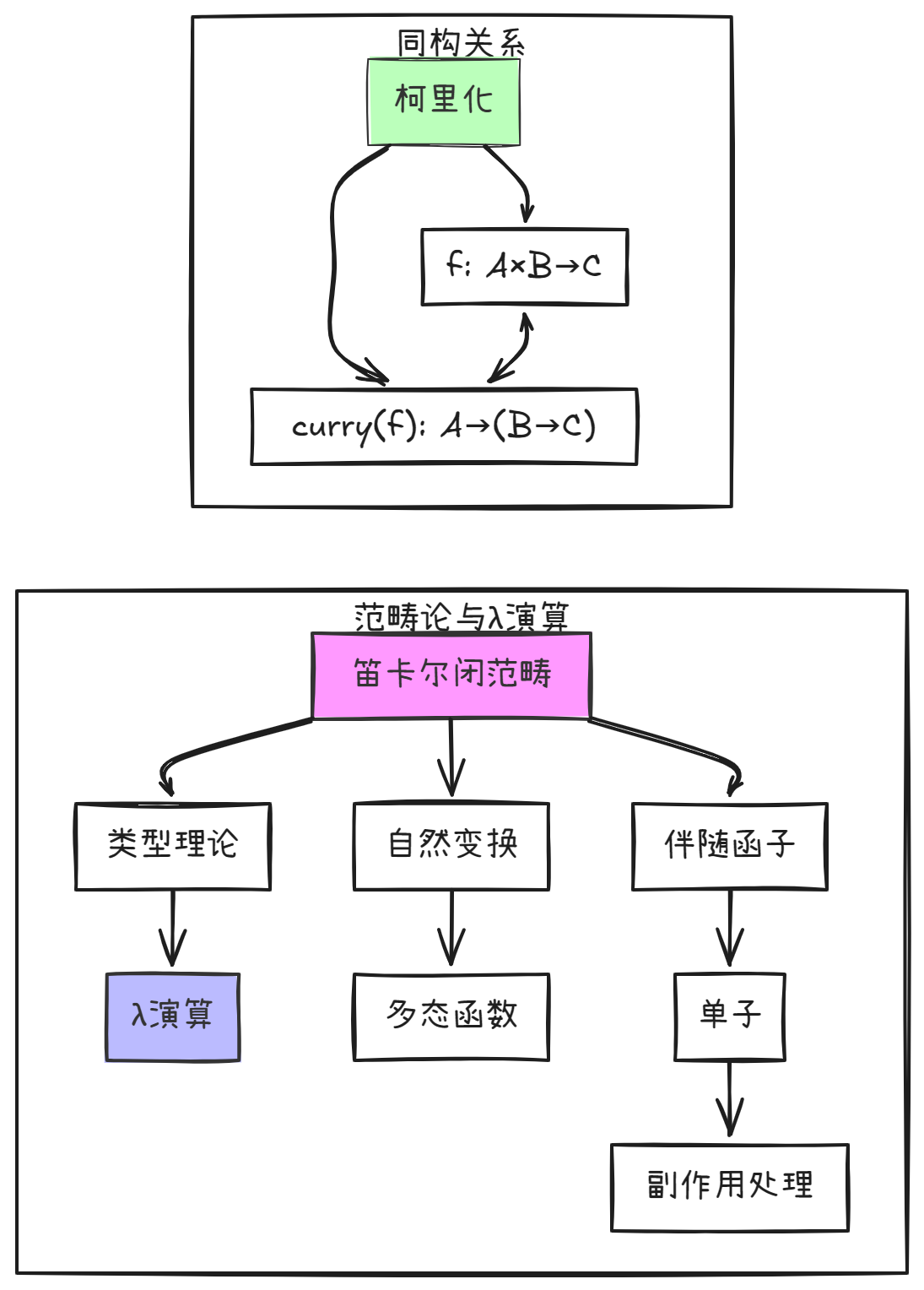
6. λ演算与范畴论的联系

另外值得一说的是，λ演算与范畴论之间存在深刻的联系，这体现在笛卡尔闭范畴（Cartesian Closed Category, CCC）中：

$$ \text{Hom}(A \times B, C) \cong \text{Hom}(A, C^B) $$

这个同构对应于λ演算中的柯里化（currying）：

$$ f: A \times B \rightarrow C \quad \Leftrightarrow \quad \text{curry}(f): A \rightarrow (B \rightarrow C) $$

7. λ演算与计算复杂性

λ演算也可以用来研究计算复杂性。例如，我们可以定义时间复杂度类：

$$ \text{TIME}(f(n)) = \{\text{语言} L \mid \exists \text{图灵机} M \text{在时间} O(f(n)) \text{内判定} L\} $$

因此对应地，我们可以在λ演算中定义类似的复杂度类，并证明它们与传统复杂度类的等价性。

8. 结论

λ演算作为一种形式化的计算模型，从简单的函数抽象和应用，到复杂的类型系统和范畴论联系，λ演算提供了一种优雅而强大的方式来理解计算的本质，我们也可以看到λ演算与图灵机虽然形式迥异，但在计算能力上是等价的，共同构成了现代计算理论的基础，随着函数式编程范式的又一次兴起，λ演算的思想将继续影响编程语言的发展和软件系统的设计。

参考文献

1. Barendregt, H. P. (1984). The Lambda Calculus: Its Syntax and Semantics. North-Holland.
2. Pierce, B. C. (2002). Types and Programming Languages. MIT Press.
3. Church, A. (1936). An unsolvable problem of elementary number theory. American Journal of Mathematics, 58(2), 345-363.
4. Hindley, J. R., & Seldin, J. P. (2008). Lambda-calculus and Combinators: An Introduction. Cambridge University Press.
5. Wadler, P. (1992). The essence of functional programming. In Proceedings of the 19th ACM SIGPLAN-SIGACT symposium on Principles of programming languages (pp. 1-14).