线性代数与数据学习：线性代数的重点

引言

本文是对线性代数核心知识的笔记整理与扩展，因为笔者最近正在学习Gilbert Strang教授的Linear Algebra and Learning from Data（中文译名：线性代数与数据学习）一书，该书的第一章着重介绍了对应用线性代数的相关知识，该章节中从多个不同矩阵分解的视角来引领读者看待线性代数的本质核心。

本系列将记录笔者在学习线代知识的同时利用Python这一工具将数学理论转化为代码实践。

矩阵向量乘积Ax与矩阵的列空间和秩

在大学线性代数课程中，我们大致可以粗略地了解到，形如$A\mathbf{x}=\mathbf{0}$的线性齐次方程组和$A\mathbf{x}=\mathbf{b}$的线性方程组中的矩阵A与向量x本质上只是记录方程组一种简略写法，例如有如下方程组：

$$ \left\{\begin{aligned} a_{1}x_{1} + b_{1}x_{2} + c_{1}x_{3} &= d_1 \\ a_{2}x_{1} + b_{2}x_{2} + c_{2}x_{3} &= d_2 \\ a_{3}x_{1} + b_{3}x_{2} + c_{3}x_{3} &= d_3 \end{aligned} \right. $$

可以写作如下矩阵方程形式：
$$\begin{bmatrix} a_{1} & b_{1} & c_{1} \\a_{2} & b_{2} & c_{2} \\a_{3} & b_{3} & c_{3} \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix} = \begin{bmatrix} d_1 \\ d_2 \\ d_3 \end{bmatrix}$$

运算前提及规则

假设有一个矩阵 $ A $ 和一个列向量 $ \mathbf{v} $，要进行矩阵与向量的乘法 $ A \mathbf{v} $，需要满足以下条件：

• 矩阵 $ A $ 的列数必须等于向量 $ \mathbf{v} $ 的行数。

  • 如果 $ A $ 是一个 $ m \times n $ 矩阵（$ m $ 行 $ n $ 列），则 $ \mathbf{v} $ 必须是一个 $ n \times 1 $ 的列向量。

设矩阵 $ A $ 和向量 $ \mathbf{v} $ 分别为：

$$ A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}, \quad \mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{bmatrix}. $$

矩阵 $ A $ 与向量 $ \mathbf{v} $ 的乘积 $ A \mathbf{v} $ 是一个新的列向量，记为 $ \mathbf{w} $，其维度为 $ m \times 1 $。具体计算方式如下：

$$ \mathbf{w} = A \mathbf{v} = \begin{bmatrix} a_{11}v_1 + a_{12}v_2 + \cdots + a_{1n}v_n \\ a_{21}v_1 + a_{22}v_2 + \cdots + a_{2n}v_n \\ \vdots \\ a_{m1}v_1 + a_{m2}v_2 + \cdots + a_{mn}v_n \end{bmatrix}. $$

换句话说，结果向量 $ \mathbf{w} $ 的第 $ i $ 个元素是矩阵 $ A $ 的第 $ i $ 行与向量 $ \mathbf{v} $ 的点积。

几何意义

在大学阶段的线代课堂里面我们可以了解到，这样的运算是具有几何意义的，因为矩阵与向量的乘法可以看作是对向量进行线性变换：

• 矩阵 $ A $ 定义了一个线性映射，将输入向量 $ \mathbf{v} $ 映射到输出向量 $ \mathbf{w} $。
• 在几何上，这对应于旋转、缩放、投影等操作。

CR分解

矩阵的 CR 分解（Column-Row Decomposition）是一种将矩阵分解为列空间和行空间的形式。对于一个 $ m \times n $ 的矩阵 $ A $，CR 分解将其表示为：

$$ A = CR $$

其中：

• $ C $ 是由 $ A $ 的线性无关列组成的子矩阵（称为列空间矩阵），其大小为 $ m \times r $，$ r $ 是矩阵 $ A $ 的秩。
• $ R $ 是一个 $ r \times n $ 的矩阵，表示这些列如何组合生成原始矩阵 $ A $。

CR 分解的核心思想是将矩阵 $ A $ 的列空间和行空间分离：

1. 列空间矩阵 $ C $：包含矩阵 $ A $ 的主元列（即线性无关的列），反映了 $ A $ 的列空间结构。
2. 行空间矩阵 $ R $：描述如何通过 $ C $ 的列线性组合生成 $ A $ 的每一列。

import numpy as np


def cr_decomposition(A):
    """
    对矩阵 A 进行 CR 分解：A = CR
    :param A: 输入矩阵 (m x n)
    :return: C (列空间矩阵), R (行空间矩阵)
    """
    # 将输入矩阵转换为 NumPy 数组
    A = np.array(A, dtype=float)

    # 使用 SVD 分解计算矩阵的秩和主元列
    U, S, Vt = np.linalg.svd(A, full_matrices=False)
    rank = np.sum(S > 1e-10)  # 根据奇异值判断矩阵的秩

    # 提取主元列作为 C 矩阵
    C = A[:, :rank]  # 取前 rank 列作为主元列

    # 构造 R 矩阵
    R = np.zeros((rank, A.shape[1]))  # 初始化 R 矩阵
    for i in range(A.shape[1]):  # 遍历 A 的每一列
        R[:, i] = np.linalg.lstsq(C, A[:, i], rcond=None)[0]  # 最小二乘法求解 R 的每一列

    return C, R

Python计算步骤：

给定一个 $ m \times n $ 的矩阵 $ A $，CR 分解的计算步骤如下：

1. 确定矩阵的秩 $ r $：

   • 使用奇异值分解（SVD）或高斯消元法计算矩阵 $ A $ 的秩 $ r $。
   • 秩 $ r $ 表示矩阵 $ A $ 中线性无关列的数量。

2. 提取主元列形成 $ C $：

   • 从矩阵 $ A $ 中选择 $ r $ 个线性无关的列，组成 $ m \times r $ 的矩阵 $ C $。

3. 构造 $ R $ 矩阵：

   • 对于 $ A $ 的每一列 $ \mathbf{a}_i $，求解最小二乘问题 $ \mathbf{a}_i = C \mathbf{x}_i $，得到系数向量 $ \mathbf{x}_i $。
   • 将所有 $ \mathbf{x}_i $ 按列排列，形成 $ r \times n $ 的矩阵 $ R $。

4. 验证分解结果：

   • 检查是否满足 $ A = CR $。在数值计算中，使用近似相等（如 np.allclose）来验证。

CR分解计算步骤总结

1. 找出独立列C，对于矩阵A而言，检查第一列是否全为0，如果不是，那么加入独立列矩阵C中，检查第二列是否为独立列第一列的倍数，如果不是加入独立列矩阵C中，检查第三列是否为独立列第一列与第二列的线性组合，如果不是加入独立列矩阵C中……以此类推。
2. 找出独立行R，因为R是矩阵A的行阶梯矩阵，可通过高斯消元法得到行空间矩阵R。

4个基本子空间

• 列空间 (Column Space)
• 行空间 (Row Space)
• 零空间 (Null Space)
• 左零空间 (Left Null Space)

列空间 (Column Space)

列空间是矩阵 $ A $ 的所有列向量的线性组合所张成的空间，记作 $ C(A) $。它是 $ \mathbb{R}^m $ 的一个子空间（假设 $ A $ 是一个 $ m \times n $ 矩阵）。

• 定义：

  $$ C(A) = \{ y \in \mathbb{R}^m \mid y = Ax, \, x \in \mathbb{R}^n \} $$

• 维度：列空间的维度等于矩阵 $ A $ 的秩 $ r $。

行空间 (Row Space)

行空间是矩阵 $ A $ 的所有行向量的线性组合所张成的空间，记作 $ C(A^T) $。它是 $ \mathbb{R}^n $ 的一个子空间。

• 定义：

  $$ C(A^T) = \{ z \in \mathbb{R}^n \mid z = A^T y, \, y \in \mathbb{R}^m \} $$

• 维度：行空间的维度也等于矩阵 $ A $ 的秩 $ r $。

零空间 (Null Space)

零空间是所有满足 $ Ax = 0 $ 的向量 $ x $ 所构成的空间，记作 $ N(A) $。它是 $ \mathbb{R}^n $ 的一个子空间。

• 定义：

  $$ N(A) = \{ x \in \mathbb{R}^n \mid Ax = 0 \} $$

• 维度：零空间的维度为 $ n - r $，其中 $ r $ 是矩阵 $ A $ 的秩。

左零空间 (Left Null Space)

左零空间是所有满足 $ A^T y = 0 $ 的向量 $ y $ 所构成的空间，记作 $ N(A^T) $。它是 $ \mathbb{R}^m $ 的一个子空间。

• 定义：

  $$ N(A^T) = \{ y \in \mathbb{R}^m \mid A^T y = 0 \} $$

• 维度：左零空间的维度为 $ m - r $，其中 $ r $ 是矩阵 $ A $ 的秩。

四个基本子空间的关系

1. 正交补关系：

   • $ C(A) $ 和 $ N(A^T) $ 是 $ \mathbb{R}^m $ 中的正交补空间。
   • $ C(A^T) $ 和 $ N(A) $ 是 $ \mathbb{R}^n $ 中的正交补空间。

2. 维数定理：

   • 对于 $ m \times n $ 矩阵 $ A $，有：

     $$ \dim(C(A)) + \dim(N(A^T)) = m $$

     $$ \dim(C(A^T)) + \dim(N(A)) = n $$

矩阵乘积 $ AB $ 和矩阵和 $ A + B $ 的秩

矩阵乘积 $ AB $ 的秩

设 $ A $ 是一个 $ m \times n $ 矩阵，$ B $ 是一个 $ n \times p $ 矩阵，则矩阵乘积 $ AB $ 是一个 $ m \times p $ 矩阵。

性质

1. 秩的不等式：
   矩阵乘积 $ AB $ 的秩满足以下不等式：

   $$ \text{rank}(AB) \leq \min(\text{rank}(A), \text{rank}(B)) $$

   这是因为 $ AB $ 的列空间是 $ A $ 的列空间的子空间，而 $ AB $ 的行空间是 $ B $ 的行空间的子空间。

2. 特殊情况：
   如果 $ A $ 或 $ B $ 是满秩矩阵（即其秩等于其行数或列数），则：

   $$ \text{rank}(AB) = \min(\text{rank}(A), \text{rank}(B)) $$

3. 零空间的关系：
   若 $ Bx = 0 $，则 $ ABx = 0 $。因此，$ B $ 的零空间是 $ AB $ 的零空间的子空间。

矩阵和 $ A + B $ 的秩

设 $ A $ 和 $ B $ 都是 $ m \times n $ 矩阵，则矩阵和 $ A + B $ 也是一个 $ m \times n $ 矩阵。

性质

1. 秩的上界：
   矩阵和 $ A + B $ 的秩满足以下不等式：

   $$ \text{rank}(A + B) \leq \text{rank}(A) + \text{rank}(B) $$

   这是因为 $ A + B $ 的列空间是 $ A $ 和 $ B $ 的列空间的线性组合。

2. 秩的下界：
   矩阵和 $ A + B $ 的秩也满足以下不等式：

   $$ \text{rank}(A + B) \geq \max(\text{rank}(A), \text{rank}(B)) - \dim(\text{Col}(A) \cap \text{Col}(B)) $$

   其中，$ \text{Col}(A) $ 表示 $ A $ 的列空间。

3. 特殊情况：
   如果 $ A $ 和 $ B $ 的列空间没有交集（即 $ \text{Col}(A) \cap \text{Col}(B) = \{0\} $），则：

   $$ \text{rank}(A + B) = \text{rank}(A) + \text{rank}(B) $$

消元法

消元法也被叫做高斯消元法 (Gaussian Elimination)，它是线性代数中求解线性方程组的一种经典方法。它通过一系列初等行变换将增广矩阵化为阶梯形矩阵（Row Echelon Form, REF）或简化阶梯形矩阵（Reduced Row Echelon Form, RREF），目的就是为了简化求解过程。

消元法的基本步骤

假设我们有一个线性方程组：

$$ \begin{aligned} a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n &= b_1, \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n &= b_2, \\ &\vdots \\ a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n &= b_m. \end{aligned} $$

对应的增广矩阵为：

$$ \left[ \begin{array}{cccc|c} a_{11} & a_{12} & \cdots & a_{1n} & b_1 \\ a_{21} & a_{22} & \cdots & a_{2n} & b_2 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} & b_m \end{array} \right] $$

步骤 1：化为阶梯形矩阵 (REF)

通过以下初等行变换将矩阵化为阶梯形矩阵：

1. 交换两行：将主元（非零元素）移到当前列的顶部。
2. 倍乘一行：将主元变为 1。
3. 倍加一行到另一行：消去主元下方的所有元素。

最终得到一个上三角形式的矩阵，例如：

$$ \left[ \begin{array}{ccc|c} 1 & a_{12}' & a_{13}' & b_1' \\ 0 & 1 & a_{23}' & b_2' \\ 0 & 0 & 1 & b_3' \end{array} \right] $$

步骤 2：化为简化阶梯形矩阵 (RREF)

进一步通过初等行变换将阶梯形矩阵化为简化阶梯形矩阵：

1. 向上消元：将主元上方的元素也消为 0。
2. 确保主元为 1：每行的主元必须为 1。

最终得到一个对角化的矩阵，例如：

$$ \left[ \begin{array}{ccc|c} 1 & 0 & 0 & x_1 \\ 0 & 1 & 0 & x_2 \\ 0 & 0 & 1 & x_3 \end{array} \right] $$

此时我们就可以直接读出解 $ x_1, x_2, x_3 $。

消元法的作用

求解线性方程组

消元法可以用于求解线性方程组的唯一解、无穷多解或无解的情况。通过观察阶梯形矩阵的最后一行，可以判断解的存在性和唯一性：

• 如果最后一行为 $ [0 \, 0 \, \cdots \, 0 \mid c] $ 且 $ c \neq 0 $，则无解。
• 如果存在自由变量（即非主元列），则有无穷多解。

矩阵的秩

通过消元法可以确定矩阵的秩（非零行的数量）。例如：

$$ \text{rank}(A) = \text{非零行的数量} $$

求逆矩阵

对于可逆矩阵 $ A $，可以通过增广矩阵 $ [A \mid I] $ 进行消元，将 $ A $ 化为单位矩阵 $ I $，同时右侧的 $ I $ 变为 $ A^{-1} $。

行图与列图

线性方程组可以通过两种不同的几何视角来理解：行图 和 列图，两种视角分别提供了不同的直观理解，我们可以更好地分析线性方程组的解。

行图 (Row Picture)

行图是从每个方程的角度来看待线性方程组。每个方程表示一个超平面（在二维空间中是直线，在三维空间中是平面），解是这些超平面的交点。

我们可以考虑以下线性方程组：

$$ \begin{aligned} x + 2y &= 4, \\ 2x - y &= 3. \end{aligned} $$

• 在二维空间中，这两个方程分别表示两条直线。
• 解是这两条直线的交点。

行图的几何意义为：

• 每个方程对应一个约束条件。
• 解的存在性和唯一性取决于这些超平面是否相交。

列图 (Column Picture)

列图是从矩阵列向量的角度来看待线性方程组，线性方程组可以写成列向量的线性组合形式：

$$ x \begin{bmatrix} a_{11} \\ a_{21} \end{bmatrix} + y \begin{bmatrix} a_{12} \\ a_{22} \end{bmatrix} = \begin{bmatrix} b_1 \\ b_2 \end{bmatrix}. $$

对于上述方程组：

$$ x \begin{bmatrix} 1 \\ 2 \end{bmatrix} + y \begin{bmatrix} 2 \\ -1 \end{bmatrix} = \begin{bmatrix} 4 \\ 3 \end{bmatrix}. $$

• $ x $ 和 $ y $ 是标量系数。
• 目标是找到合适的 $ x $ 和 $ y $，使得两个列向量的线性组合等于右侧的向量。

列图的几何意义为：

• 列图展示了如何通过调整系数 $ x $ 和 $ y $ 来“拼凑”出目标向量。
• 如果目标向量不在列空间中，则方程组无解。

可视化意义

我们可以通过Python绘图展示行图与列图的可视化意义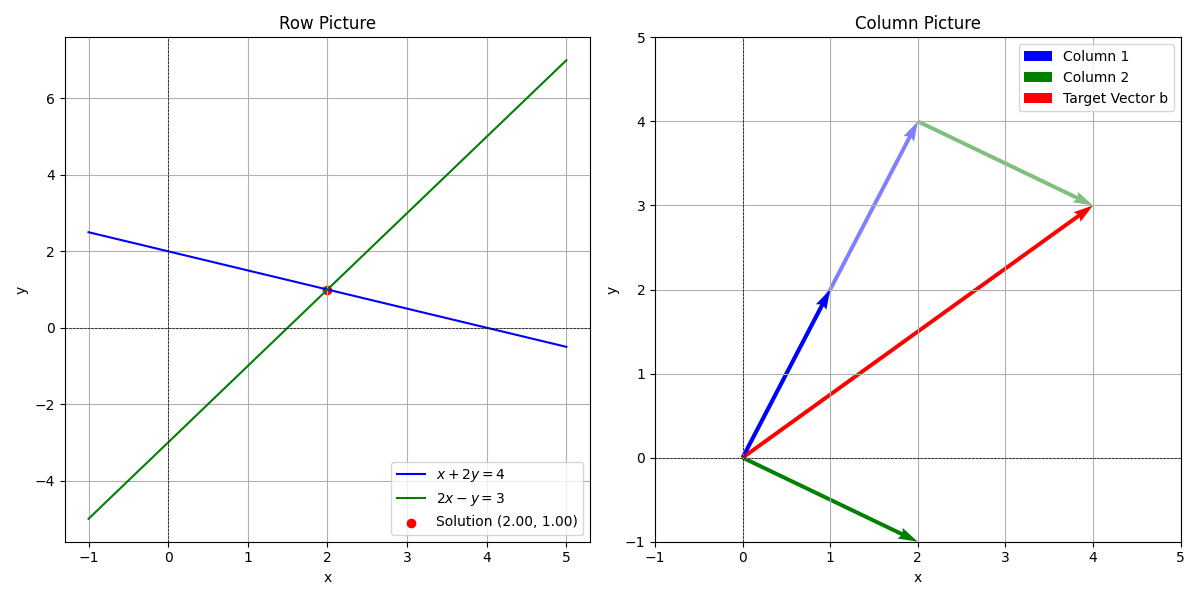

import numpy as np
import matplotlib.pyplot as plt

# 线性方程组的系数矩阵和右侧向量
A = np.array([[1, 2], [2, -1]])
b = np.array([4, 3])

# 计算解
solution = np.linalg.solve(A, b)
x_sol, y_sol = solution

# 行图 (Row Picture)
plt.figure(figsize=(12, 6))

# 绘制第一条直线 x + 2y = 4
x_vals = np.linspace(-1, 5, 100)
y1 = (4 - x_vals) / 2

# 绘制第二条直线 2x - y = 3
y2 = 2 * x_vals - 3

plt.subplot(1, 2, 1)
plt.plot(x_vals, y1, label="$x + 2y = 4$", color="blue")
plt.plot(x_vals, y2, label="$2x - y = 3$", color="green")
plt.scatter(x_sol, y_sol, color="red", label=f"Solution ({x_sol:.2f}, {y_sol:.2f})")
plt.axhline(0, color="black", linewidth=0.5, linestyle="--")
plt.axvline(0, color="black", linewidth=0.5, linestyle="--")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Row Picture")
plt.legend()
plt.grid()

# 列图 (Column Picture)
plt.subplot(1, 2, 2)

# 绘制列向量
col1 = A[:, 0]
col2 = A[:, 1]

plt.quiver(0, 0, col1[0], col1[1], angles='xy', scale_units='xy', scale=1, color="blue", label="Column 1")
plt.quiver(0, 0, col2[0], col2[1], angles='xy', scale_units='xy', scale=1, color="green", label="Column 2")

# 绘制目标向量 b
plt.quiver(0, 0, b[0], b[1], angles='xy', scale_units='xy', scale=1, color="red", label="Target Vector b")

# 绘制线性组合
plt.quiver(0, 0, x_sol * col1[0], x_sol * col1[1], angles='xy', scale_units='xy', scale=1, color="blue", alpha=0.5)
plt.quiver(x_sol * col1[0], x_sol * col1[1], y_sol * col2[0], y_sol * col2[1], angles='xy', scale_units='xy', scale=1, color="green", alpha=0.5)

plt.xlim(-1, 5)
plt.ylim(-1, 5)
plt.axhline(0, color="black", linewidth=0.5, linestyle="--")
plt.axvline(0, color="black", linewidth=0.5, linestyle="--")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Column Picture")
plt.legend()
plt.grid()

plt.tight_layout()
plt.show()

LU分解与高斯消元法

高斯消元法和 LU 分解是线性代数中求解线性方程组的两种重要方法。它们之间有着密切的关系：LU 分解可以看作是对高斯消元法的一种矩阵形式化描述。

在上一小节我们提到，高斯消元法通过初等行变换将矩阵 $ A $ 化为上三角矩阵 $ U $，从而简化线性方程组的求解过程。
现仍然假设我们有这样一个线性方程组：

$$ A \mathbf{x} = \mathbf{b}, $$

其中 $ A $ 是一个 $ n \times n $ 矩阵，$ \mathbf{x} $ 和 $ \mathbf{b} $ 是 $ n $ 维向量。

高斯消元法的核心步骤

1. 前向消元：通过初等行变换将 $ A $ 化为上三角矩阵 $ U $。
2. 回代求解：从 $ U \mathbf{x} = \mathbf{c} $ 中回代求解 $ \mathbf{x} $。

LU 分解的概念

LU 分解（Lower-Upper Decomposition）是将矩阵 $ A $ 分解为一个下三角矩阵 $ L $ 和一个上三角矩阵 $ U $ 的乘积：

$$ A = LU, $$

其中：

• $ L $ 是单位下三角矩阵（对角线元素为 1）。
• $ U $ 是上三角矩阵。

LU 分解的意义

• LU 分解将矩阵 $ A $ 的信息存储在 $ L $ 和 $ U $ 中。
• 通过 LU 分解，可以高效地求解多个具有相同系数矩阵 $ A $ 但不同右侧向量 $ \mathbf{b} $ 的线性方程组。

高斯消元法与LU分解的关系

高斯消元法的过程实际上隐含了 LU 分解的思想，具体来说就是：

1. 高斯消元法中的初等行变换：

   • 在高斯消元法中，每一步初等行变换都可以用一个初等矩阵 $ E_i $ 表示。

   • 整个消元过程可以写成一系列初等矩阵的乘积：

     $$ E_k E_{k-1} \cdots E_1 A = U, $$

     其中 $ U $ 是上三角矩阵。

2. LU 分解的构造：

   • 初等矩阵的逆矩阵 $ E_i^{-1} $ 是下三角矩阵。

   • 将所有初等矩阵的逆矩阵相乘，得到下三角矩阵 $ L $：

     $$ L = E_1^{-1} E_2^{-1} \cdots E_k^{-1}. $$

   • 因此，矩阵 $ A $ 可以分解为：

     $$ A = LU. $$

3. 求解线性方程组：

   • 使用 LU 分解后，原方程组 $ A \mathbf{x} = \mathbf{b} $ 转化为两个简单的三角形方程组：

     $$ L \mathbf{y} = \mathbf{b}, \quad U \mathbf{x} = \mathbf{y}. $$

   • 这两个方程组可以通过前向替换和回代快速求解。

LU 分解举例

给定矩阵 $ A $：

$$ A = \begin{bmatrix} 2 & 1 & 1 \\ 4 & 3 & 3 \\ 8 & 7 & 9 \end{bmatrix}. $$

通过高斯消元法，我们可以得到：

$$ L = \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 4 & 3 & 1 \end{bmatrix}, \quad U = \begin{bmatrix} 2 & 1 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 2 \end{bmatrix}. $$

验证：

$$ LU = \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 4 & 3 & 1 \end{bmatrix} \begin{bmatrix} 2 & 1 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 2 \end{bmatrix} = \begin{bmatrix} 2 & 1 & 1 \\ 4 & 3 & 3 \\ 8 & 7 & 9 \end{bmatrix} = A. $$

以下给出Python对于LU分解的代码实现

import numpy as np

def lu_decomposition(A):
    """
    实现 LU 分解：将矩阵 A 分解为 L 和 U。
    :param A: 输入的 n x n 矩阵
    :return: 下三角矩阵 L 和上三角矩阵 U
    """
    n = len(A)
    # 初始化 L 和 U
    L = np.eye(n)  # 单位下三角矩阵
    U = np.zeros((n, n))  # 上三角矩阵

    # 高斯消元法逐步构造 U 和 L
    for j in range(n):  # 遍历列
        # 计算 U 的第 j 列
        for i in range(j, n):
            U[i, j] = A[i, j] - sum(L[i, k] * U[k, j] for k in range(i))

        # 计算 L 的第 j 行
        for i in range(j + 1, n):
            L[i, j] = (A[i, j] - sum(L[i, k] * U[k, j] for k in range(j))) / U[j, j]

    return L, U

事实上，在Python的科学计算函数库scipy.linalg.lu包中已经具有了这样的LU分解函数，因此我们也可以直接调用其方法进行LU分解：

import numpy as np
from scipy.linalg import lu

# 定义矩阵 A
A = np.array([[2, 1, 1],
              [4, 3, 3],
              [8, 7, 9]])

# LU 分解，P (置换矩阵)，L (下三角矩阵)，U (上三角矩阵)，A = PLU
P, L, U = lu(A)


# 验证 
reconstructed_A = P @ L @ U
print("验证 A 的 LU 构造矩阵:\n", reconstructed_A)

LU 分解中的置换矩阵

在 LU 分解中，置换矩阵 (Permutation Matrix) $ P $ 用于处理主元为零或数值不稳定的情况，借助置换矩阵，可以让分解过程的数值稳定性变得更好，并避免因主元过小而导致的误差。

置换矩阵 $ P $ 是一个特殊的方阵，它的每一行和每一列有且仅有一个元素为 1，其余元素为 0。
置换矩阵的作用就是对矩阵的行进行重新排列。

给定一个 $ 3 \times 3 $ 的置换矩阵：

$$ P = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}, $$

它将矩阵的第 1 行与第 2 行交换。

引入置换矩阵的原因

1. 避免主元为零：

   • 如果在高斯消元过程中遇到主元为零，则无法继续分解。
   • 通过行交换（即置换矩阵），可以找到非零主元。

2. 提高数值稳定性：

   • 在数值计算中，选择绝对值最大的主元（部分选主元）可以减少舍入误差。

带置换矩阵的 LU 分解步骤

1. 初始化：

   • 初始化 $ L $ 为单位矩阵，$ U $ 为零矩阵。
   • 初始化 $ P $ 为单位矩阵。

2. 部分选主元：

   • 在每一步消元前，找到当前列中绝对值最大的元素所在的行。
   • 将该行与当前行交换，并更新置换矩阵 $ P $。

3. 高斯消元：

   • 按照高斯消元法逐步构造 $ L $ 和 $ U $。

以下代码手动实现了带置换矩阵的 LU 分解：

import numpy as np

def lu_decomposition_with_pivoting(A):
    """
    手动实现带置换矩阵的 LU 分解：PA = LU。
    :param A: 输入的 n x n 矩阵
    :return: 置换矩阵 P，下三角矩阵 L，上三角矩阵 U
    """
    n = len(A)
    # 初始化 L、U 和 P
    L = np.eye(n)  # 单位下三角矩阵
    U = np.zeros((n, n))  # 上三角矩阵
    P = np.eye(n)  # 置换矩阵

    # 高斯消元法逐步构造 U 和 L
    for j in range(n):  # 遍历列
        # 部分选主元：找到当前列中绝对值最大的元素所在的行
        max_row = np.argmax(np.abs(A[j:, j])) + j
        if max_row != j:
            # 交换 A 的行
            A[[j, max_row]] = A[[max_row, j]]
            # 更新置换矩阵 P
            P[[j, max_row]] = P[[max_row, j]]
            # 如果之前已经计算了 L 的部分，也需要交换
            if j > 0:
                L[[j, max_row], :j] = L[[max_row, j], :j]

        # 计算 U 的第 j 列
        for i in range(j, n):
            U[i, j] = A[i, j] - sum(L[i, k] * U[k, j] for k in range(i))

        # 计算 L 的第 j 列
        for i in range(j + 1, n):
            L[i, j] = (A[i, j] - sum(L[i, k] * U[k, j] for k in range(j))) / U[j, j]

    return P, L, U

LU分解数学公式

通过高斯消元法，我们可以逐步构造 $ L $ 和 $ U $：

• 对于上三角矩阵 $ U $，其元素 $ U[i, j] $ 计算如下：

  $$ U[i, j] = A[i, j] - \sum_{k=1}^{i-1} L[i, k] \cdot U[k, j]. $$

• 对于下三角矩阵 $ L $，其非对角线元素 $ L[i, j] $ 计算如下（当 $ i > j $ 时）：

  $$ L[i, j] = \frac{A[i, j] - \sum_{k=1}^{j-1} L[i, k] \cdot U[k, j]}{U[j, j]}. $$

最终，带置换矩阵的 LU 分解可以写成：

$$ PA = LU. $$

LU分解过程需要注意的点

矩阵必须是非奇异的

• 如果矩阵 $ A $ 是奇异矩阵（行列式为 0），则 LU 分解可能失败。
• 在实际应用中，可以通过部分选主元来增强数值稳定性。

数值稳定性

• 在数值计算中，选择绝对值最大的主元（部分选主元）可以减少舍入误差。
• 如果不进行选主元操作，可能会导致分解结果不稳定，尤其是在主元接近零的情况下。

时间复杂度

• LU 分解的时间复杂度为 $ O(n^3) $，适合中小型矩阵。
• 对于大型稀疏矩阵，可以考虑使用专门的稀疏矩阵算法。

置换矩阵的性质

• 置换矩阵 $ P $ 是正交矩阵，满足 $ P^T P = I $。
• 置换矩阵的逆等于其转置：$ P^{-1} = P^T $。

正交矩阵及其子空间

正交矩阵

定义

一个方阵 $Q \in \mathbb{R}^{n \times n}$ 被称为正交矩阵，当且仅当其满足：
$Q^\top Q = QQ^\top = I$
其中 $I$ 为单位矩阵，$Q^\top$ 表示矩阵的转置。

核心性质

1. 列/行正交性：矩阵的列向量组和行向量组均为标准正交向量组，即：

   • 对列向量 $\mathbf{q}_i, \mathbf{q}_j$，有 $\mathbf{q}_i^\top \mathbf{q}_j = \delta_{ij}$
   • 其中 $\delta_{ij}$ 为克罗内克函数（$i=j$ 时为 1，否则为 0）

2. 保内积与长度：对于任意向量 $\mathbf{x}, \mathbf{y}$：

   • $(Q\mathbf{x})^\top (Q\mathbf{y}) = \mathbf{x}^\top \mathbf{y}$
   • $\|Q\mathbf{x}\| = \|\mathbf{x}\|$
3. 行列式：$\det(Q) = \pm 1$

子空间（Subspace）

定义

向量空间 $\mathbb{R}^n$ 的非空子集 $S$ 称为子空间，当其满足：

1. 加法封闭性：若 $\mathbf{u}, \mathbf{v} \in S$，则 $\mathbf{u} + \mathbf{v} \in S$
2. 数乘封闭性：若 $\mathbf{u} \in S, c \in \mathbb{R}$，则 $c\mathbf{u} \in S$

常见子空间

1. 列空间（Column Space）：

   • 矩阵 $A \in \mathbb{R}^{m \times n}$ 的列向量的所有线性组合：
     $C(A) = \{ A\mathbf{x} \mid \mathbf{x} \in \mathbb{R}^n \}$

2. 零空间（Null Space）：

   • 齐次方程 $A\mathbf{x} = \mathbf{0}$ 的解集：
     $N(A) = \{ \mathbf{x} \in \mathbb{R}^n \mid A\mathbf{x} = \mathbf{0} \}$

3. 行空间（Row Space）：

   • 矩阵 $A$ 的行向量生成的子空间：$C(A^\top)$

4. 正交补子空间：

   • 设 $S \subseteq \mathbb{R}^n$，其正交补定义为：
     $S^\perp = \{ \mathbf{v} \in \mathbb{R}^n \mid \mathbf{v}^\top \mathbf{u} = 0, \forall \mathbf{u} \in S \}$

重要性质

• 维数定理：对于矩阵 $A \in \mathbb{R}^{m \times n}$：$\dim C(A) + \dim N(A) = n$
• 正交分解：$\mathbb{R}^n = C(A^\top) \oplus N(A)$
  其中 $\oplus$ 表示直和。

例如：

• $\mathbb{R}^3$ 中过原点的平面是一个二维子空间
• 矩阵 $A = \begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}$ 的列空间为 $\mathbb{R}^2$